A beginners guide to Dynamic Programming

Arjhun S

@arjunta_varudhu

Please make sure you have a working understanding of recursion before you begin

I personally struggled to understand dynamic programming for quite a bit. This guide is mainly to give people a kickstart. Please note that this is not an extensive and exhaustive guide to dynamic programming but a straightforward one aimed to give the reader a strong fundamental grasp on the idea. I was taught all these fancy and widely known problems like N-queens, 01 knapsack, etc. They have standard dynamic programming solutions which look extremely intuitive to me right now, but I used to break my head to get a grasp of them once upon a time. I definitely don’t want that for you!

Dynamic programming, to be put in simple terms is a means of reducing the time complexity of problems where repetitive computations occur. It is done by storing these repetitive computations and reusing them instead of re-computing them and, thereby, increasing the space complexity. The tradeoff is acceptable.

Before, getting into the details of DP, I strongly suggest you to understand backtracking.

Backtracking is a systematic way of exploring all potential solutions to a problem by trying out different choices and eliminating the ones that don’t work.

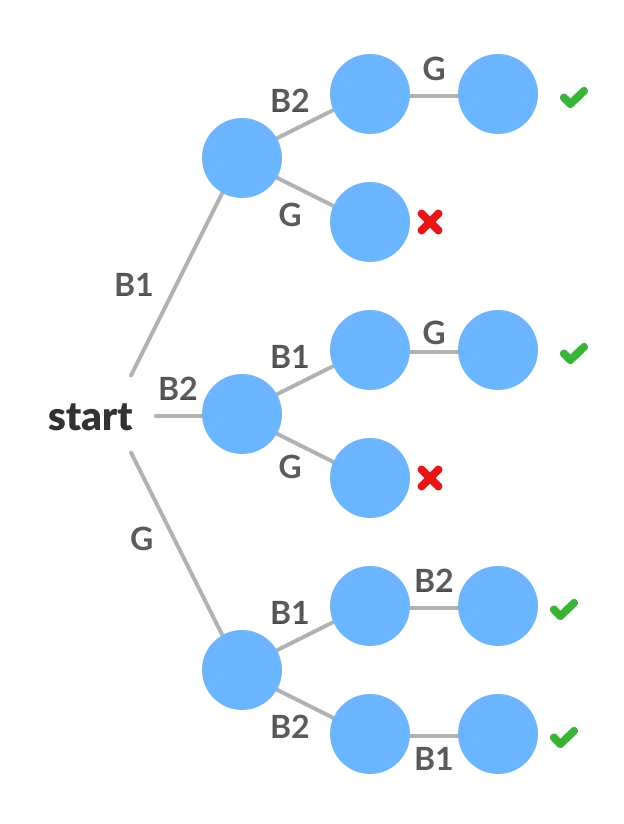
Look at this image if you’re confused. Ignore the notations and look at the crosses and ticks. At some point, the choices have become acceptable as they brought you to a solution. You would be right if you deduced that backtracking could be used in problems where there could be multiple solutions and exhaustive search (backtracking is nothing but a fancy word for brute-force). A simple example would be finding out of one string is a permutation of another string or not. The brute-force solution would be to permute in all ways possible and simultaneously compare with the other string and return a boolean. This is exactly the backtracking solution.

(Or we could count the frequencies of the individual characters xD)

Anyway, hope that gave you a fundamental idea on backtracking. Now let’s talk about how it translates to DP.

You should understand the difference in approach here. Backtracking talks about trying out all permutations/combinations and, on the other hand, DP talks about how you can store some of these computations somewhere and reuse when required again. The latter is a way of optimising your solution.

Note that while some backtracking problems can indeed be improved with DP, not all can be. In order to be able to use DP, we need the problem to hold an important characteristic — overlapping subproblems.

What are overlapping subproblems?

In many dynamic programming problems, the original problem can be broken down into smaller, more manageable subproblems. As the algorithm progresses, it recursively solves these subproblems to find their solutions. However, it’s possible that the same subproblem is encountered multiple times during this recursive process.

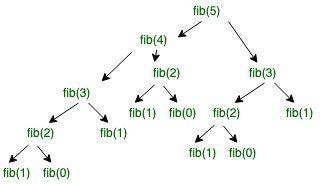
The above image is a recursion tree of the fibonacci function. If you look closely, you can notice how many times the fib(2) is called.

def fib(n):
    if n <= 1:
        return n
  
    return fib(n - 1) + fib(n - 2)

fib(5)

This repetitive call essentially makes your time complexity exponential — O(2^N).

The whole idea of DP is to store this result somewhere and reuse it later.

Let’s modify the above function to work with DP.

def fib(n, arr):
    if n <= 1:
        return n
    
    if arr[n] != -1:
        return arr[n]
    
    arr[n] = fib(n-1, arr) + fib(n-2, arr)
    return arr[n]

This approach is known as memoization. You don’t really need to worry about the terms now. Try to understand how it works by yourself.

Memoization involves passing an extra array filled with -1, except for the first 2 values since we already know them (0 and 1, the initial Fibonacci numbers). The function takes a top-down approach, starting from 5 and moving down to 0. At each step, it checks whether the corresponding array element is populated (i.e., not equal to -1). If it is, then the value must have been computed by some earlier function call, so the function simply returns it. Otherwise, it calculates the Fibonacci value and assigns it to the respective element in the array.

By implementing this memoization technique, we can avoid redundant computations and improve the time complexity of the Fibonacci calculation. This approach effectively combines the benefits of recursion with the efficiency of storing previously computed results to achieve a relatively more optimal solution.

We could also modify this to work in a bottom-up manner

def fib(n, arr):
    for i in range(2, n + 1):
        arr[i] = arr[i - 1] + arr[i - 2]
      
    return arr[n]

This is essentially a faster and simpler solution where you sequentially calculate the next value using the previous 2 values in the array. You could initialise the first two elements in the array as 0 and 1 and that’s it.

We have an incredibly efficient solution because of dynamic programming!

Understanding the concept of solving the Fibonacci problem efficiently is crucial in tackling more complex dynamic programming (DP) problems, such as those found on LeetCode. To approach a new DP problem, start by drawing a recursion tree to identify repetitive computations. This visual representation helps in understanding the recursive nature of the problem and potential overlapping subproblems.

Begin solving the problem with a brute force recursive solution, which may have exponential time complexity due to redundant calculations. Next, improve the solution using memoization, a technique to store previously computed results in a data structure like a dictionary. Memoization ensures that repeated computations are avoided, reducing the time complexity significantly.

After implementing the memoization solution, proceed to convert it into a bottom-up approach. In this technique, you iteratively calculate and store the results for smaller subproblems until you reach the final solution. This eliminates the need for recursion and often provides a more efficient solution.

It’s essential to practice solving DP problems through these steps to gain an intuitive understanding of the patterns and optimal solutions. With enough practice, you can become more proficient and solve complex DP problems directly, without needing to go through all the intermediate steps.

I hope this article helps you grasp the basic concepts of dynamic programming. The topic can be complex, but a simple explanation like this can be beneficial for those who may have struggled with it, especially when taught in a challenging and stupid manner (I was taught DP before backtracking 🤦🏻). By mastering dynamic programming and backtracking, you can efficiently solve a wide range of algorithmic problems.

Anyway, thanks for reading through.

Cheers.

PS: Fibonacci does not really need DP.

def fibonacci(n):
    if n <= 1:
        return n

    prev, curr = 0, 1
    for _ in range(2, n + 1):
        prev, curr = curr, prev + curr

    return curr

This essentially solves fibonacci in linear time and constant space.